Decimals Whole Numbers and Exponents
- Details
- Parent Category: Math League Website
- Published: 15 September 2008
Decimals, Whole Numbers, and Exponents
Decimal numbers
Whole number portion
Expanded form of a decimal number
Adding decimals
Subtracting decimals
Comparing decimal numbers
Rounding decimal numbers
Estimating sums and differences
Multiplying decimal numbers
Dividing whole numbers, with remainders
Dividing whole numbers, with decimal portions
Dividing decimals by whole numbers
Dividing decimals by decimals
Exponents (powers of 2, 3, 4, ...)
Factorial notation
Square roots
Decimal Numbers
Decimal numbers such as 3.762 are used in situations which call for more precision than whole numbers provide.
As with whole numbers, a digit in a decimal number has a value which depends on the place of the digit. The places to the left of the decimal point are ones, tens, hundreds, and so on, just as with whole numbers. This table shows the decimal place value for various positions:
Note that adding extra zeros to the right of the last decimal digit does not change the value of the decimal number.
Place (underlined)
Name of Position
1.234567
Ones (units) position
1.234567
Tenths
1.234567
Hundredths
1.234567
Thousandths
1.234567
Ten thousandths
1.234567
Hundred Thousandths
1.234567
Millionths
Example:
In the number 3.762, the 3 is in the ones place, the 7 is in the tenths place, the 6 is in the hundredths place, and the 2 is in the thousandths place.
Example:
The number 14.504 is equal to 14.50400, since adding extra zeros to the right of a decimal number does not change its value.
Whole Number Portion
The whole number portion of a decimal number are those digits to the left of the decimal place.
Example:
In the number 23.65, the whole number portion is 23.
In the number 0.024, the whole number portion is 0.
Expanded Form of a Decimal Number
The expanded form of a decimal number is the number written as the sum of its whole number and decimal place values.
Example:
3 + 0.7 + 0.06 + 0.002 is the expanded form of the number 3.762.
100 + 3 + 0.06 is the expanded form of the number 103.06.
Adding Decimals
To add decimals, line up the decimal points and then follow the rules for adding or subtracting whole numbers, placing the decimal point in the same column as above.
When one number has more decimal places than another, use 0's to give them the same number of decimal places.
Example:
76.69 + 51.37
1) Line up the decimal points:
76.69
+51.37
2) Then add.
76.69
+51.37
128.06
Example:
12.924 + 3.6
1) Line up the decimal points:
12.924
+ 3.600
2) Then add.
12.924
+ 3.600
16.524
Subtracting Decimals
To subtract decimals, line up the decimal points and then follow the rules for adding or subtracting whole numbers, placing the decimal point in the same column as above.
When one number has more decimal places than another, use 0's to give them the same number of decimal places.
Example:
18.2 - 6.008
1) Line up the decimal points.
18.2
- 6.008
2) Add extra 0's, using the fact that 18.2 = 18.200
18.200
- 6.008
3) Subtract.
18.200
- 6.008
12.192
Comparing Decimal Numbers
Symbols are used to show how the size of one number compares to another. These symbols are < (less than), > (greater than), and = (equals). To compare the size of decimal numbers, we compare the whole number portions first. The larger decimal number is the one with the lager whole number portion. If the whole number parts are both equal, we compare the decimal portions of the numbers. The leftmost decimal digit is the most significant digit. Compare the pairs of digits in each decimal place, starting with the most significant digit until you find a pair that is different. The number with the larger digit is the larger number. Note that the number with the most digits is not necessarily the largest.
Example:
Compare 1 and 0.002. We begin by comparing the whole number parts: in this case 1>0, 0 being the whole number part of 0.002, and so 1>0.002.
Example:
Compare 0.402 and 0.412. The numbers 0.402 and 0.412 have the same number of digits, and their whole number parts are both 0. We compare the next most significant digit of each number, the digit in the tenths place, 4 in each case. Since they are equal, we go on to the hundredths place, and in this case, 0<1, so 0.402<0.412.
Example:
Compare 120.65 and 34.999. Comparing the whole number parts, 120>34, so 120.65>34.999.
Example:
Compare 12.345 and 12.097. Since the whole number parts are both equal, we compare the decimal portions starting with the tenths digit. Since 3>0, we have 12.345>12.097.
Note:
Remember that adding extra zeros to the right of a decimal does not change its value:
2.4 = 2.40 = 2.400 = 2.4000.
Rounding Decimal Numbers
To round a number to any decimal place value, we want to find the number with zeros in all of the lower places that is closest in value to the original number. As with whole numbers, we look at the digit to the right of the place we wish to round to. Note: When the digit 5, 6, 7, 8, or 9 appears in the ones place, round up; when the digit 0, 1, 2, 3, or 4 appears in the ones place, round down.
Examples:
Rounding 1.19 to the nearest tenth gives 1.2 (1.20).
Rounding 1.545 to the nearest hundredth gives 1.55.
Rounding 0.1024 to the nearest thousandth gives 0.102.
Rounding 1.80 to the nearest one gives 2.
Rounding 150.090 to the nearest hundred gives 200.
Rounding 4499 to the nearest thousand gives 4000.
Estimating Sums and Differences
We can use rounding to get quick estimates on sums and differences of decimal numbers. First round each number to the place value you choose, then add or subtract the rounded numbers to estimate the sum or difference.
Example:
To estimate the sum 119.36 + 0.56 to the nearest whole number, first round each number to the nearest one, giving us 119 + 1, then add to get 120.
Multiplying Decimal Numbers
Multiplying decimals is just like multiplying whole numbers. The only extra step is to decide how many digits to leave to the right of the decimal point. To do that, add the numbers of digits to the right of the decimal point in both factors.
Example:
4.032 × 4
We can multiply 4032 by 4 to get 16128. There are three decimal places in 4.032, so place the decimal three digits from the right:
4.032 × 4 = 16.128
Example:
6.74 × 9.063
We can multiply 674 by 9063 to get 6108462. Then there are 5 decimal places: two in the number 6.74 and three in the number 9.063, so place the decimal five digits from the right:
6.74 × 9.063 = 61.08462.
Dividing Whole Numbers, with Remainders
Example:
1400 ÷ 7..
Since 14 ÷ 7 = 2, and 1400 is 100 times greater than 14, the answer is 2 × 100 = 200.
Many problems are similar to the above example, where the answer is easily obtained by adding on or taking off an appropriate number of 0's. Others are more complicated.
Example:
4934 ÷ 6. Use long division.
So the answer is 822 with a remainder of 2, written 822 R2.
To double-check that the answer is correct, multiply the quotient by the divisor and add the remainder:
(822 × 6) + 2 = 4932 + 2 = 4934.
Dividing Whole Numbers, with Decimal Portions
Example:
Find 32 ÷ 6 to the nearest whole number.
32 ÷ 6 = 5 r2. 6 is the divisor; 2 is the remainder.
2 is closer to 0 than 6, so round down. The answer is 5.
Dividing Decimals by Whole Numbers
To divide a decimal by a whole number, use long division, and just remember to line up the decimal points:
Example:
13.44 ÷ 12.
When rounding an answer, divide one place further than the place you're rounding to, and round the result. Add 0's to the right of the number being divided, if necessary.
Example:
1.0 ÷ 6. Round to the nearest thousandth.
To round 0.16666 . . . to the nearest thousandth, we take 4 places to the right of the decimal point and round to 3 places. Here, we round 0.1666 to 0.167, the answer.
Dividing Decimals by Decimals
To divide by a decimal, multiply that decimal by a power of 10 great enough to obtain a whole number. Multiply the dividend by that same power of 10. Then the problem becomes one involving division by a whole number instead of division by a decimal.
Example:
0.144 ÷ 0.12
Multiplying the divisor (0.12) and the dividend (0.144) by 100, then dividing, gives the same result.
The answer is 1.2.
Be aware that some problems are less difficult and do not require this procedure.
Example:
6 ÷ 2.00
This is the same as 6 ÷ 2! The answer is 3.
Exponents (Powers of 2, 3, 4, ...)
Exponential notation is useful in situations where the same number is multiplied repeatedly. The notation is often shown as "^"
The number being multiplied is called the base, and the exponent tells how many times the base is multiplied by itself.
Example:
4 ×4 ×4 ×4 ×4 ×4 = 46
The base in this example is 4, the exponent is 6.
We refer to this as four to the sixth power, or four to the power of six, written as 4^6.
Examples:
2 ×2 ×2 = 2^3 = 8
1.1"2 = 1.1 × 1.1 = 1.21
0.5^3 = 0.5 × 0.5 × 0.5 = 0.125
10^6 = 10 × 10 × 10 × 10 × 10 × 10 = 1000000
Observe that the base may be a decimal.
Special Cases:
A number with an exponent of two is referred to as the square of a number.
The square of a whole number is known as a perfect square. The numbers 1, 4, 9, 16, and 25 are all perfect squares.
A number with an exponent of three is referred to as the cube of a number.
The cube of a whole number is known as a perfect cube. The numbers 1, 8, 27, 64, and 125 are all perfect cubes.
Note:
A number written with an exponent of 1 is the same as the given number.
23^1 = 23.
Factorial Notation n!
The product of the first n whole numbers is written as n!, and is the product
1 × 2 × 3 × 4 × … × (n - 1) × n.
Examples:
4! = 1 × 2 × 3 × 4 = 24
11! = 1 × 2 × 3 × 4 × 5 × 6 × 7 × 8 × 9 × 10 × 11 = 39916800
Tricks:
When dividing factorials, note that many of the numbers cancel out!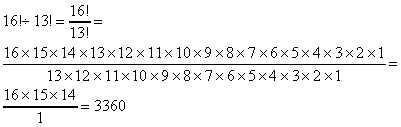
Note:
The number 0! Is defined to be 1.
Square Roots
The square root of a whole number n is the number r with the property that r × r = n.
We write this as
.
We say that the number n is the square of the number r.
Examples:
The square root of 9 is 3, since 3 × 3 = 9.
The square root of 289 is 17, since 17 × 17 = 289.
The square root of 2 is close to 1.41421. We say close to because the digits to the right of the decimal point in the square root of 2 continue forever, without any repeating pattern. Such a number is called an irrational number, meaning that it cannot be written as a fraction.
Tricks:
Since the square root of a whole number n is the number r with the property that r × r = n, we always have
That is, the square of the square root of any number is just the original number.
We also have, for any number r that the square root of the square of r is the absolute value of r.
We say the absolute value, because the notation actually means the positive square root of n.
Example:
From the example above, we see that each positive number n actually has 2 numbers r that satisfy r × r = n, one is positive, and the other is negative.




